2021.04.07 - [데이터 사이언티스트/딥러닝] - 신경망 학습방법과 역전파(BP)
신경망 학습방법과 역전파(BP)
이번 포스트는 신경망의 학습방법과 역전파의 개념에 대해 다뤄보겠습니다. 신경망의 학습방법의 경우 2번 가중치 부분은 사전학습모델을 사용할 경우 달라질 수 있습니다. 역전파를 코드로도
ksh950510.tistory.com
앞선 글에서 GD가 나오게 된 계기를 설명했습니다.
요즘은 다들 Adam optimizer만 쓰는데 Adam이 어떤 optimizer를 계승해서 나오게됐는지 살펴보겠습니다.
Optimizer

<Gradient descent(GD)>
가장 기본이 되는 optimizer 알고리즘으로 경사를 따라 내려가면서 W를 update시킨다.


GD를 사용하는 이유
왜 이렇게 기울기를 사용하여 step별로 update를 시키는것일까?
애초에 cost(W)식을 미분하여 0인 점을 찾으면 되는게 아닌가??
-> 내가 알고 있기로 두 가지 이유 때문에 closed form으로 해결하지 못한다고 알고 있다.
1. 대부분의 non-linear regression문제는 closed form solution이 존재하지 않다.
2. closed form solution이 존재해도 수많은 parameter가 있을때는 GD로 해결하는 것이 계산적으로도 더 효율적이다.
비선형 문제와 파라미터가 많을때 사용
<Stochastic gradient decent(SGD)>
full-batch가 아닌 mini batch로 학습을 진행하는 것
(* batch로 학습하는 이유 : full-batch로 epoch마다 weight를 수정하지 않고 빠르게 mini-batch로 weight를 수정하면서 학습하기 위해)

<Momentum>
SGD에 momentum개념을 추가한 것이다.
현재 batch로만 학습하는 것이 아니라 이전의 batch 학습결과도 반영한다.

Momentum notation1

Momentum notation2
Momentum이 없는 경우)

Momentum이 없는 경우
두번째 학습에서 가중치 변화량은 0.3이다.
Momentum추가한 경우)

Momentum 추가
Momentum을 추가하여 이전의 학습결과도 반영하기 때문에 두번째 학습에서 가중치 변화량은 0.75이다.
(* 이번 batch에 의해 학습이 크게 좌지우지 되지 않게하기 위해 이전까지의 학습결과를 보통 0.9반영하고 이번 batch는 0.1만 반영한다.)
<AdaGrad>
학습을 통해 크게 변동이 있었던 가중치에 대해서는 학습률을 감소시키고 학습을 통해 아직 가중치의 변동이 별로 없었던 가중치는 학습률을 증가시켜서 학습이 되게끔 한다.

AdaGrad notation
기존 SGD에서의 notation에서 h가 추가되었는데 h는 가중치 기울기 제곱들을 더해간다.
따라서 가중치 값에 많은 변동이 있었던 가중치는 점점 학습률을 감소시키게 된다.
(*AdaGrad는 무한히 학습하면 어느 순간 h가 너무 커져서 학습이 아예 안될 수 있다. 이를 RMSProp에서 개선한다.)
<RMSProp>
AdaGrad는 간단한 convex function에서 잘 동작하지만, 복잡한 다차원 곡면 function에서는 global minimum에 도달하기 전에 학습률이 0에 수렴할 수 있다. 따라서 RMSProp에서는 이를 보완하였다.
a) 가중치 기울기를 단순 누적시키는 것이 아니라 최신 기울기들이 더 반영되도록 한다.

RMSProp notation
AdaGrad의 h에 hyper parameter p가 추가되었다. p가 작을수록 가장 최신의 기울기를 더 크게 반영한다.
Momentum에서와 반대로 이번 batch에 의한 최신 기울기가 크게 반영되도록 한다. (누적 h보다 최신 기울기에 초점)
즉, 그동안 가중치에 큰 변동사항이 있었어도 이번 batch로 인한 기울기가 완만하면 학습률을 높인다.
-> (minimum과 같은 극점 근처에서 학습 속도가 느려지는 문제와 local minimum에 수렴하는 문제를 해결)
* 최신 batch가 이전 batch중 특정 1개보다 더 크게 반영된다는 점은 같다.
(Momentum에서는 이번 batch에 의해 크게 좌지우지 되지 않도록 한다. / 지금까지 누적된 momentum에 초점)
b) hyper parameter p를 추가하여 h가 무한히 커지지 않게 한다.
p*h + (1-p)g^2 연산을 하므로 h가 가질 수 있는 값이 max{g^2} 으로 bounded된다는 것을 알 수 있다.
<Adam>
Momentum과 RMSProp를 융합한 방법이다. 먼저 Adam optimizer의 수도코드는 아래와 같다.

출처: https://arxiv.org/pdf/1412.6980.pdf
Momentum과 Adagrad는 각각 v와 h가 처음에 0으로 초기화되면 W가 학습 초반에 0으로 biased되는 문제가 있다.

Momentum notation1

RMSProp notation
이런 잘못된 초기화로 인해 0으로 biased되는 문제를 해결하기 위해 Adam이 고안되었다.
위 수도코드에서 (m=Momentum에서의 v, v=RMSProp에서의 h, g=W의 기울기) 라고 보면된다.
아래 예시들을 보면서 어떻게 Adam이 위 문제들을 해결했는지 보자.
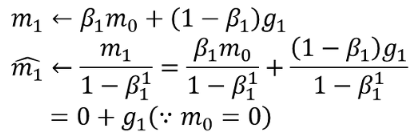
출처 : https://light-tree.tistory.com/141?category=755497
기존 Momentum에서는 m0가 0으로 초기화되면 m1=0.1g1( ∵β1 = 0.9) 으로써 0으로 biased된다.
그러나 Adam에서는 m/(1-β)로 m을 update하기 때문에 m1=g1이 되어 0으로 biased됨을 해결하였다.

출처 : https://light-tree.tistory.com/141?category=755497
또한 위 m2가 update되는 식을 보면 알 수 있듯이 최신 기울기 한 개에 의해 update가 좌지우지 되지 않도록 하여 Momentum의 성질을 그대로 따르고 있다.
위 수도코드를 보면 RMSProp 방식인 v parameter 역시 동일한 방식으로 0으로 biased됨을 해결하고 있다.

출처 : https://light-tree.tistory.com/141?category=755497
마지막 실질적인 W update 식을 보면 RMSProp에서와 같이 v를 루트를씌워서 나눠주고 거기에 Momentum을 곱하는 형식으로 update하고 있다.
Loss Funtion
비용(cost), 손실(loss) 함수 계산
한 데이터 샘플을 Forward Propagation를 시키고 마지막 출력층을 통과한 값과
이 데이터의 타겟값(label)을 비교하여 loss(or error)를 계산합니다.
여기서 한 데이터 포인트에서의 손실을 loss라 하고 전체 데이터 셋의 loss를 합한 개념을 cost라고 합니다.
1. BinaryCrossentropy
실제 레이블과 예측 레이블 간의 교차 엔트로피 손실을 계산한다. 2개의 레이블 클래스(0, 1로 가정)가 있을 때 Binary Crossentropy를 사용하면 좋다.
2. CategoricalCrossentropy
레이블 클래스가 2개 이상일 경우 사용된다. 보통 softmax 다음에 연계되어 나온다고 하여 softmax 활성화 함수 다음에 나온다고 하여 softmax loss 라고도 불린다.
3. SparseCategoricalCrossentropy
훈련 데이터의 label(target)이 one-hot vector 이면 CategoricalCrossentropy
훈련 데이터의 label(target)이 정수이면 SparseCategoricalCrossentropy
를 사용하면 됩니다.
4. MeanSquaredError
예측한 값과 실제 값 사이의 평균 제곱 오차를 정의한다. 공식이 매우 간단하며, 차가 커질수록 제곱 연산으로 인해서 값이 더욱 뚜렷해진다. 그리고 제곱으로 인해서 오차가 양수이든 음수이든 누적 값을 증가시킨다.
옵티마이저와 손실함수는 모든 신경망(RNN, CNN, GAN)에 쓰입니다.
코드를 구동하다 보면 자연스레 익숙해지고 colab에서는 적절한 손실함수를 추천해주는 기능도 있습니다.
optimizer와 loss funtion외에도 모델의 성능을 높이는 방법인 학습규제전략(Regularization Strategies)이란게 있습니다.
이를 다음 포스트에서 살펴보겠습니다.
'데이터 분석 > 딥러닝' 카테고리의 다른 글
| [python] ArgumentParser(argparse) 정리 (0) | 2023.08.03 |
|---|---|
| Compound Scaling (0) | 2021.11.18 |
| 신경망 학습방법과 역전파(BP) (0) | 2021.04.07 |
| Neural Network (0) | 2021.04.06 |


