신경망 Neural Network
신경망(Neural Networks)은 1943년경 뇌의 신경활동을 수학으로 표현한 아이디어와
1957년 Rosenblatt이 고안한 Perceptron(퍼셉트론) 알고리즘이 발전해서 현재의 신경망 개념에 이르게 되었습니다.
1970년대에 신경망에 대한 연구가 많이 진행됐지만 많은 한계점들로 인해 잠시 신경망 연구가 중단됐으나,
최근들어 한계점을 극복하게 되면서 많은 연구가 이루어지고 있습니다. (ex. XOR -> 다층퍼셉트론으로 해결)
현대의 신경망은 Artificial Neural Networks(ANN, 인공신경망)이라고 불리는 학습 모델이며 뇌의 실제 신경계의 특징을 모사하여 만들어진 계산 모델(computational model)입니다.
- 신경세포(Neuron)

뉴런은 수상돌기(Dendrites)에서 입력신호(다른 뉴런과의 시냅스)를 받아 신경세포 내에서 정보를 통합하고 임계값을 통과하면 축삭돌기(Axon)로 최종 출력 신호를 전송(또 다른 뉴런으로 전파)합니다.
위의 뇌 신경망의 작은 구조인 신경세포(Neuron)를 모사한 인공 뉴런으로 불리는
퍼셉트론은 다수의 입력 신호를 받아 하나의 신호를 출력하는 구조입니다.
- 퍼셉트론

(위 그림에서 '원형'으로 표현된 것을 뉴런 or 노드(node)라고 부릅니다.)
입력신호(x0, x1, ...)가 뉴런에 입력되면 각각 고유한 가중치(weights, w0, w1, ...)가 곱해지는데
가중치는 시냅스(synapses)의 연결강도(시냅스의 두께, 개수)와 같은 역할을 합니다.
편향(bias)은 natural neuron과 다른 인공 뉴런 퍼셉트론만의 특징
입력 신호와 가중치의 내적 값들과 bias를 모두 합한 값이 정해진 임계값(threshold)을 넘을 경우에만
다음 노드들이 있는 Layer로 신호가 전달됩니다.
여기서 기억해야 할 것은 인공신경망이 우리 신경계를 얼마나 잘 모사하느냐가 아니라 인공신경망을 이용해서
데이터에서 발견할 수 있는 복잡한 관계를 학습할 수 있는 강력한 알고리즘과 데이터 구조를 만드는 것 입니다.
활성화 함수 (Activation function)
앞에서 본 퍼셉트론이 신경망이 되기 위해서는 활성 함수(Activation function)를 사용해야 합니다.
활성 함수는 비선형(non-linear)함수라고도 불립니다.
신경망은 활성 함수의 비선형성을 통해 네트워크는 더 복잡한 현실의 데이터 및 문제를 학습하고 표현할 수 있습니다.
활성 함수는 뉴런의 입력과 가중치의 내적인 출력(퍼셉트론의 output)에 요소별로 적용됩니다.
먼저 가장 기본적인 활성 함수 3가지를 배워보겠습니다.
계단함수(Step function)
import numpy as np
import matplotlib.pyplot as plt
import math
# 샘플 데이터를 확인합니다.
x = np.array([-1, 1, 2])
print(x)
# 0보다 큰가?
y = x>0
print(y)
# 논리형태를 0과 1로 표현해보기
y = y.astype(np.int)
print(y)
###
[-1 1 2]
[False True True]
[0 1 1]
###import numpy as np
import matplotlib.pyplot as plt
import math
# 샘플 데이터를 확인합니다.
x = np.array([-1, 1, 2])
print(x)
# 0보다 큰가?
y = x>0
print(y)
# 논리형태를 0과 1로 표현해보기
y = y.astype(np.int)
print(y)
###
[-1 1 2]
[False True True]
[0 1 1]
#### 함수 정의
def step_function(x):
return np.array(x>0, dtype=np.int)
# 그래프 그리기
x = np.linspace(-1, 1, 100) # 지정된 간격 동안 균등 한 간격의 숫자를 반환합니다. 시작, 중지, 숫자
plt.step(x, step_function(x))
plt.show() 
시그모이드(Sigmoid)함수
0보다 작을수록 출력이 0에 수렴하고, 0보다 클수록 출력이 1에 수렴하는 함수
# 함수정의
def sigmoid(x):
return 1/ (1+np.exp(-x))
x = np.array([-5, -1, 0, 0.1, 5, 500000])
print(sigmoid(x))
###
[0.00669285 0.26894142 0.5 0.52497919 0.99330715 1. ]
###x = np.linspace(-10, 10, 100)
plt.plot(x, sigmoid(x))
plt.xlabel("x")
plt.ylabel("Sigmoid(X)")
plt.show()

ReLU 함수 (Rectified Linear Unit)
대부분의 이론책에서는 Sigmoid를 가장 많이 배우지만 실제로 가장 많이 사용하는 것은 ReLU입니다.
z = np.arange(-3, 3, .1)
zero = np.zeros(len(z))
y = np.max([zero, z], axis=0)
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(z, y)
ax.set_ylim([-1.0, 3.0])
ax.set_xlim([-3.0, 3.0])
#ax.grid(True)
ax.set_xlabel('z')
ax.set_title('ReLU: Rectified linear unit')
plt.show()
fig = plt.gcf()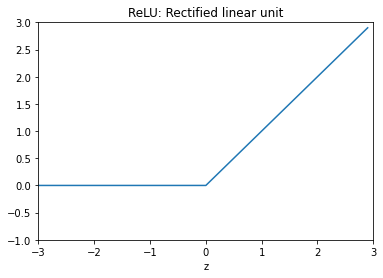
(tanh 함수, softmax 함수 등의 함수들도 실전에서 자주 쓰이지만 함수의 형태는 sigmoid와 비슷해서 생략)
softmax 함수는 입력값(뉴런의 output)의 총합을 1로 치환, output들을 0 ~ 1사이로 고정 (output을 확률로 나타낼때 사용)
tanh 함수는 시그모이드와 비슷하지만 출력의 범위가 -1 ~ +1 사이
지금까지 신경망의 기본 구조에 대해 알아보았습니다.
신경망은 뉴런이라 불리는 노드가 기초 유닛입니다.
노드들은 입력신호를 받을 수 있으며 가중치라 불리는 엣지들로 연결되어 있고 다음 노드에 출력을 전달합니다.
노드의 output은 입력신호와 가중치를 내적한 값에 활성화 함수를 적용한 값입니다.
뒤에 배우지만 노드의 output은 다음 층에 있는 노드의 input이 됩니다.
이 노드들의 연결 구조 조합이 신경망을 구성합니다.
위에서 배운 신경망은 여러 층(layers)으로 구성됩니다.
Layer들은 기본적으로 입력층(input layers), 은닉층(hidden layers), 출력층(output layers) 으로 나뉩니다.
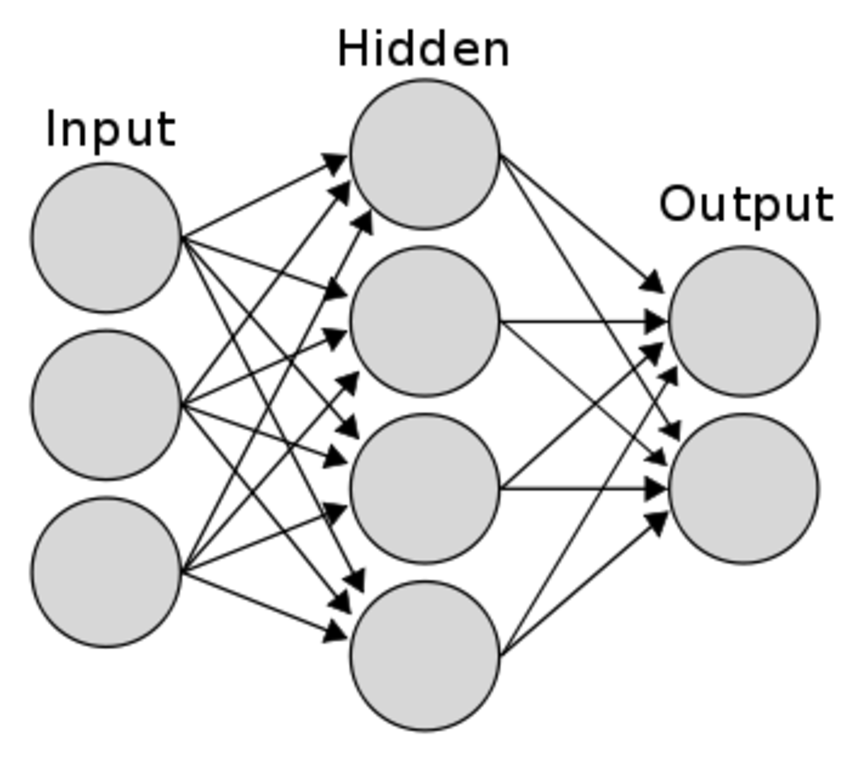
입력층(Input Layers)
입력층은 데이터셋으로부터 입력을 받습니다. 입력 변수의 수와 입력 노드의 수는 같습니다.
보통 입력층은 어떤 계산도 수행하지 않고 그냥 값들을 전달하기만 하는 특징을 가지고 있습니다.
그래서 신경망의 층수(깊이, depth)를 셀 때 입력층은 포함하지 않습니다. 위의 신경망은 2층이라고 할 수 있습니다.
(책 별로 입력층까지 포함하여 depth를 표현할때도 있지만 거의 다 입력층은 제외한 층수를 depth로 설정)
은닉층(Hidden Layers)
계산이 일어나는 층이 둘 이상인 신경망을 다층(multilayer) 신경망 이라고 부르는데
계산이 없는 입력층과 마지막 출력층 사이에 있는 층들을 은닉층(Hidden Layers) 이라고 부릅니다.
은닉층에 있는 계산의 결과를 사용자가 볼 수 없기(hidden) 때문에 이런 이름이 붙었습니다.
(계산결과를 보려면 볼 순 있는데 복잡한 신경망일수록 사람이 해석하기는 힘듦, 신경망이 블랙박스라고도 불리는 이유)
은닉층에는 변수 수(입력과 출력의 수)와 상관 없이 다수의 노드가 포함 가능합니다.
딥러닝(deep learning)은 사실 두 개 이상의 은닉층(이때 부터 깊다(deep)라고 합니다)들을 가진 신경망, 입력층을 제외하고 시작하여 3개 이상의 Layer를 갖는 신경망을 의미합니다.
현대의 딥러닝은 은닉층의 개수를 늘리고 층 내부의 연결과 학습 방법을 달리하여 이전보다 더 복잡한 데이터의 구조를 학습했습니다. 이 방법을 통해서 딥러닝은 과거 신경망들의 성능 기록들을 갱신했고, 그로 인해 딥러닝에 대한 연구가 활발하게 이루어지게 되었습니다.
고차원 신경망의 장점 :
https://colah.github.io/posts/2014-03-NN-Manifolds-Topology/
출력층(Output Layers)
신경망 가장 마지막 층이 출력층 입니다. 대부분의 출력층에는 활성화 함수(activation function)가 존재하는데 활성화 함수는 보통 풀고자 하는 문제에 따라 다른 종류를 사용합니다.
- 회귀(Regression) 문제에서 예측할 목표 변수가 실수값인 경우 활성화 함수가 필요하지 않으며 출력노드의 수는 출력변수의 갯수와 같습니다.
- 이진 분류(binary classification) 문제의 경우 시그모이드(sigmoid) 함수를 사용해서 출력을 확률 값으로 변환하여 label을 결정하도록 합니다.
- 다중클래스(multi-class)를 분류하는 경우 출력층 노드가 부류 수 만큼 존재하며 소프트맥스(softmax) 함수를 활성화 함수로 사용합니다.
python으로 신경망 구현
W는 가중치이고, B는 bias인데, 바이어스는 노드마다 하나씩 들어간다.
그림과는 다르지만, 마지막 W3, B3는 아웃풋을 출력하기 전 하나의 레이어를 더 거친다는 개념으로
임의로 추가한것 (huristic하게 설정하면 되고, 출력값에만 맞춰주면 됩니다.)
# 네트워크 구조 생성 함수 정의
def init_network():
network = {}
network['W1'] = np.array([[0.1, 0.3, 0.5, 0.7], [0.1, 0.3, 0.5, 0.7], [0.2, 0.4, 0.6, 0.8]]) # 3 x 4
network['B1'] = np.array([0.11, 0.12, 0.13, 0.14])
network['W2'] = np.array([[0.1, 0.5], [0.2, 0.6], [0.3, 0.4], [0.35, 0.35]]) # 4 x 2
network['B2'] = np.array([0.1, 0.5])
network['W3'] = np.array([[0.1, 0.5], [0.2, 0.6]]) # 2 x 2
network['B3'] = np.array([0.1, 0.5])
return networkW는 가중치이고, B는 bias인데, 바이어스는 노드마다 하나씩 들어간다.
그림과는 다르지만, 마지막 W3, B3는 아웃풋을 출력하기 전 하나의 레이어를 더 거친다는 개념으로
임의로 추가한것 (huristic하게 설정하면 되고, 출력값에만 맞춰주면 됩니다.)
# 순전파 함수 정의
def forward(network, x):
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['B1'], network['B2'], network['B3']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
z2 = sigmoid(a2)
a3 = np.dot(z2, W3) + b3
y = a3
return y# 네트워크 제작
network = init_network()
# 샘플 데이터
x = np.array([1, 0.5, 0.7])
# 순전파 실행
y = forward(network, x)
print(y)신경망은 노드들이 가중치로 연결되어 입력값을 출력값으로 내보내는 계산 함수(computation function)의 일종이며,
노드들의 가중치값인 parameter를 찾는 과정을 학습(training, learning)이라고 합니다.
Tensorflow 신경망 예제
import pandas as pd
#!pip install tensorflow-gpu==2.0.0-rc1
import tensorflow as tf# 라이브러리 데이터셋을 불러옵니다.
mnist = tf.keras.datasets.mnist
# Training Set, Test Set을 분류해줍니다.
(x_train, y_train), (x_test, y_test) = mnist.load_data()
# Value normalization을 수행합니다.
x_train, x_test = x_train / 255.0, x_test / 255.0# 신경망 모델을 구축합니다.
model = tf.keras.models.Sequential([
tf.keras.layers.Flatten(input_shape=(28, 28)), # 784개의 노드로 변경해주는 layer
tf.keras.layers.Dense(128, activation='relu'), # 784개의 노드가 128개의 노드를 만나서 784*128개의 parameter를 만듬
tf.keras.layers.Dropout(0.2), # 존재목적 Overfitting 방지, layer들의 연결성을 랜덤하게 끊어주는것
tf.keras.layers.Dense(10, activation='softmax') # 마지막 layer로 10개의 출력으로 맞춰주는것
# softmax는 다른 뉴런의 출력값과의 상대적인 비교를 통해 최종출력값이 결정되는데,
# 보통 문자인식이나 숫자 인식과 같은 분류목적 신경망의 최종단에 softmax함수를 쓴다.(해당 값이 나올 확률을 알 수 있음)
])
# 구축한 모델을 컴파일하며, 옵티마이저, loss function 등을 설정해줍니다.
model.compile(optimizer='adam',
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
## 학습을 하는 부분입니다. 다음 시간에 배우게될 Bp에 대해서 이해를 하신다면 이 과정이 이해가 될 것입니다.
model.fit(x_train, y_train, epochs=5) # epoch의 수를 변화시키며 더 많이 학습하거나 적게 학습할 수 있습니다.
## 만들어진 모델을 이용하여 예측하는 부분입니다.
model.evaluate(x_test, y_test, verbose=2) ## 테스트 과정28*28을 flatten하게 바꿔주고, 128개의 노드는 huristic하게 설정
6만개의 데이터에 대해 epoch을 2번했다면 총 12만개의 데이터를 학습한것
iteration과 다른 개념
epoch을 진행할수록 accuracy는 올라가고 loss는 줄어듭니다
tf.keras.layers.Dense(units, ...)
# Dense에 들어가는 옵션
units,
activation = None,
use_bias = True,
kernel_initializer = 'glorot_uniform',
bias_iniotializer = 'zeros',
kernel_regularizer = None,
bias_regularizer = None,
activity_regularizer = None,
kernel_constraint = None,
bias_constraint = None,
**kwargs- units : 출력 값의 크기
- activation : 활성화 함수
- use_bias : 편향(b)을 사용할지 여부
- kernel_initializer : 가중치(W) 초기화 함수
- bias_iniotializer : 편향 초기화 함수
- kernel_regularizer : 가중치 정규화 방법
- bias_regularizer : 편향 정규화 방법
- activity_regularizer : 출력 값 정규화 방법
- kernel_constraint : 가중치에 적용되는 부가적인 제약 함수
- bias_constraint : 편향에 적용되는 부가적인 제약 함수
www.tensorflow.org/api_docs/python/tf/keras/layers
Module: tf.keras.layers | TensorFlow Core v2.4.1
Keras layers API.
www.tensorflow.org
인공신경망은 선형 회귀 알고리즘과 다릅니다
여기서 선형 회귀 문제를 신경망을 통해 풀어본 이유는 가중치, bias등의 신경망 기초 개념과 구조에 익숙해지기 위함입니다.
그리고 앞으로 배울 순방향 신경망(feedforward NN)을 학습할 때 손실 함수(Loss function)를 통해 예측값과 실제값의 차이를 평가하고 경사 하강법(Gradient Descent)을 통해 최적의 가중치, bias를 찾는 개념을 쉽게 이해하기 위해서 입니다.
Python으로 만드는 신경망 학습
지금 구현해볼 퍼셉트론은 Rosenblatt이 처음 개발했던 모습과는 다릅니다. 계단함수 대신 비선형 시그모이드함수를 사용하는 다층신경망과 유사하게 만들어 보겠습니다.
# 학습데이터를 생성합니다
np.random.seed(827)
# 입력 벡터: [x0, x1]
# X: 입력(inputs)
X = np.array([
[0, 0]
,[1, 1]
,[1, 0]
,[0, 1]
])
# bias
b = 1
# Y: 타겟값(correct outputs)
Y= np.array([[0],[1],[1],[1]])초기 가중치는 무작위(Random)
입력데이터와 가중치 연산
활성화 함수를 사용해 학습군(epoch)의 출력
# W: [weight0, weight1]
W = 2 * np.random.rand(2,1) - 1
array([[-0.36561912],
[-0.48951912]])
# Z: 가중합
Z = np.dot(X, W) + b
array([[1. ],
[0.14486176],
[0.63438088],
[0.51048088]])
# A: 출력(activated outputs)
A = sigmoid(Z)
array([[0.73105858],
[0.53615224],
[0.65348215],
[0.6249192 ]])출력 오차를 줄이기 위한 역전파(경사하강법 이용)
에러를 계산하기 위해 실제 타겟 값과 출력값의 차를 계산합니다.
경사하강법은 손실값에 대한 미분값을 사용하여 최저의 손실값을 가지는 매개변수(가중치)를 찾는 방법 입니다.
그리고 역전파 알고리즘은 경사하강법에 필요한 미분값을 빠르고 효율적으로 찾는 알고리즘입니다.
지금은 이 방법을 코드로 이용하는 부분만 살펴 보시기 바랍니다.
에러 계산에는 MSE 비용함수(cost function)을 사용할 때, 가중치에 대해 도함수를 구하면 (sebastianraschka)

와 같은 형태가 되고 oi 를 wj에 관해 편미분 하면

라고 쓸 수 있습니다. 벡터 계산 코드로 구현하면 다음과 같고 이를 가중치 업데이트에 사용합니다.
# da: 에러값, dE/da
# dz: dE/dz
# dw: 가중치 업데이트 값
# db: bias 업데이트 값
da = A - Y
dz = da * sigmoid_prime(Z)
dw = np.dot(X.T, dz)
db = np.sum(da, keepdims=True)
print(dw)
print(db)
[[-0.19382232]
[-0.20327284]]
[[-0.45438783]]X.T
array([[0, 1, 1, 0],
[0, 1, 0, 1]])
dz
array([[ 0.14373484],
[-0.1153557 ],
[-0.07846662],
[-0.08791714]])
db
array([[-0.45438783]])
print('기존 가중치: \n',W)
기존 가중치:
[[-0.36561912]
[-0.48951912]]
# 가중치 업데이트(batch)
W += dw
b += db
print('업데이트 후 가중치: \n', W)
print('업데이트 후 bias: \n', b)
업데이트 후 가중치:
[[-0.55944144]
[-0.69279195]]
업데이트 후 bias:
[[0.54561217]]
loss 값에 따라 가중치와 bias가 업데이트 되는 방향이 달라집니다.
반복(iteration)을 통한 정교한 가중치 생성
# 이미 입력 데이터와 타겟 출력은 윗 부분에서 선언 하였습니다.
# 가중치 초기화
# W = 2 * np.random.random((2,1)) - 1
W = np.random.randn(2,1)
# W = np.zeros((2,1))
b = 0
print('학습 전 가중치: \n', W)
# 가중치 업데이트를 10,000회 (10,000 epoch) 진행하겠습니다.
for iteration in range(1000):
# 순방향 전파
Z = np.dot(X, W) + b
A = sigmoid(Z)
# 역방향 전파(기울기 계산)
da = Y - A
dz = da * sigmoid_prime(Z)
dw = np.dot(X.T, dz)
db = np.sum(da, keepdims=True)
W += dw
b += db
print('학습 후 가중치: \n', W)
print('학습 후 bias: \n', b)
print('학습 후 예측값: \n', A.round(3))
학습 전 가중치:
[[-0.26203003]
[ 0.47949834]]
학습 후 가중치:
[[5.92195632]
[5.9220684 ]]
학습 후 bias:
[[-2.5909238]]
학습 후 예측값:
[[0.07 ]
[1. ]
[0.965]
[0.965]]Review
- 퍼셉트론의 이해 : 입력 값 = 2 개이상, 출력 값 = 1 개
- 다층(Multi-Layer) 퍼셉트론의 개념과 딥러닝의 차이점을 설명할 수 있다.
- 신경망의 기본 구조에 대해서 설명할 수 있다.
- 뉴런(노드)
- 연결(가중치,엣지)
- 입력/은닉/출력층
- 활성함수 : 비선형성을 만들어 주는 구조
- 퍼셉트론의 학습과정을 통해서 학습되는 것은 가중치와 bias이다.
- 분류/회귀 정의 리뷰, 결정경계
드래그시 정답이 보입니다.
요약
활성화 함수를 사용하면 입력값에 대한 출력값이 linear하게 나오지 않으므로 선형분류기를 비선형 시스템으로 만들 수 있다.
* MLP(Multiple layer perceptron)는 단지 linear layer를 여러개 쌓는 개념이 아닌 활성화 함수를 이용한 non-linear 시스템을 여러 layer로 쌓는 개념이다.
결론적으로 활성화 함수는 입력값을 non-linear한 방식으로 출력값을 도출하기 위해 사용한다.
이를 통해 linear system을 non-linear한 system으로 바꿀 수 있게 되는 것이다.
활성화함수를 사용하면 왜 입력값에 대한 출력값을 비선형으로 만들 수 있는지는 함수의 생김새만 봐도 명확하다.
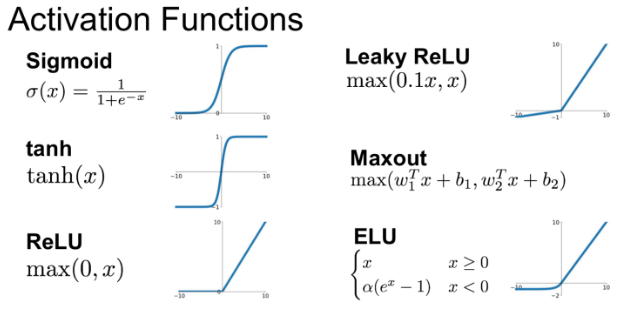
그러나, 이렇게 활성화 함수를 이용하여 비선형 시스템인 MLP를 이용하여 XOR는 해결될 수 있지만, MLP의 파라미터 개수가 점점 많아지면서 각각의 weight와 bias를 학습시키는 것이 매우 어려워 다시 한 번 침체기를 겪게되었다.
그리고 이를 해결한 알고리즘이 바로 역전파(Back Propagation)이다.
'데이터 분석 > 딥러닝' 카테고리의 다른 글
| [python] ArgumentParser(argparse) 정리 (0) | 2023.08.03 |
|---|---|
| Compound Scaling (0) | 2021.11.18 |
| Optimizer, Loss Funtion (0) | 2021.04.08 |
| 신경망 학습방법과 역전파(BP) (0) | 2021.04.07 |


