이번 포스트는 신경망의 학습방법과 역전파의 개념에 대해 다뤄보겠습니다.
신경망의 학습방법의 경우 2번 가중치 부분은 사전학습모델을 사용할 경우 달라질 수 있습니다.
역전파를 코드로도 구현해서 덧붙였습니다. (역전파의 가장 중요한 부분인 chain rule만 이해하셔도 됩니다.)
만약 틀린부분이 있다면 댓글달아주시면 감사하겠습니다.
신경망 학습 방법
오늘은 조금 더 깊이 있게 신경망 훈련 방법에 대해서 살펴볼 것 입니다. 순방향 신경망(FP)과 같은 다층퍼셉트론(MLP, Multi-layer Perceptron) 구조의 신경망은 경사하강법(Gradient descent, GD)으로 학습을 할 수 있는데 역전파(Backpropagationm, BP) 알고리즘에 의해 필요한 기울기(gradient)계산이 가능합니다.
신경망 구조에 대해 다시 간략히 짚어보겠습니다:

- 입력층(Input layer), 은닉층(Hidden layer), 출력층(output layer)이 존재합니다.
- 각 층은 n 개의 뉴런(노드, activation units)으로 구성되어 있고 각각 가중치(weight)와 편향(bias)를 가지고 있습니다.
- 왼쪽 입력층에서부터 오른쪽으로 층에서 층으로 데이터가 전달되는데 다음과 같습니다:
- 훈련데이터를 입력층으로부터(이전 층으로부터) 받습니다.
- 입력데이터는 가중치와 가중합(weighted sum)을 합니다.
- 편향(bias)이 더해집니다.
- 편향이 더해진 가중합은 활성화함수(activation function)를 통해 다음 층으로 전달됩니다. 입력의 특성이 n개인 경우 전달되는 값은 다음식과 같습니다.
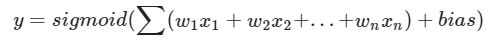
신경망 학습 알고리즘 요약:
- 학습할 신경망 구조를 선택합니다.
- 입력층 유닛의 수 = 특징 수
- 출력층 유닛의 수 = 타겟 클래스 수
- 은닉층 수, 각 은닉층의 노드 수
- 가중치 랜덤 초기화
- 순방향 전파를 통해 출력층 y값을 모든 입력 x에 대해 계산합니다.
- 비용함수를 계산합니다.
- 역방향 전파를 통해 편미분 값들을 계산합니다.
- 경사하강법 (or 다른 최적화 알고리즘)을 역전파와 함께 사용하여 비용함수를 최소화 합니다.
- 어떤 중지 기준(Early stop)을 충족하거나 비용함수를 최소화 할 때까지 단계 2-5를 반복합니다. 2-5를 한 번 진행하는 것을 epoch 또는 iteration이라 말합니다.
(batch_size에 따라 달라집니다, 전체데이터셋을 모두 학습했을때 1 epoch)
ex) 총 데이터가 100개, batch size가 10이면,
1 iteration = 10개 데이터에 대해서 학습
1 Epoch = 100/batch size = 10 iteration
비용(cost), 손실(loss) 함수 계산
한 데이터 샘플을 Forward Propagation를 시키고 마지막 출력층을 통과한 값과
이 데이터의 타겟값(label)을 비교하여 loss(or error)를 계산합니다.
여기서 한 데이터 포인트에서의 손실을 loss라 하고 전체 데이터 셋의 loss를 합한 개념을 cost라고 합니다.
Backpropagation (BP)
역전파(Backpropagation)는 "Backwards Propagation of errors"의 줄임말 입니다. 신경망에 존재하는 가중치들을 어떻게 업데이트 해야할지 결정하기 위해 epoch/batch 마다 출력층에서 입력층 방향(역방향)으로 미분값을 계산하고 가중치를 업데이트 하여 신경망을 학습하는 알고리즘입니다. 지금까지 배운 알고리즘 중 가장 복잡한 수식을 보여주는데 미분법에 대한 이해가 약간 필요합니다. 역전파과정의 수식에 대한 설명은 영상들을 꼭 참고하여 주시기 바랍니다.

예제를 통해서 이해해보자
데이터는 선형함수를 통해서 나왔다고 가정합시다
y=5x1+2x2+40
x1: 공부시간
x2: 수면시간
# 해당 코드는 선형함수를 예측하는 예제입니다.
import numpy as np
np.random.seed(812)
# [공부시간, 수면시간]
X = np.array(([8,8],
[2,5],
[7,6]), dtype=float)
# 시험 점수
y = X[:,0]*5 + X[:,1]*2 # 뒤에서 정규화 코드를 거치므로 +40은 빼주었습니다.
y = y.reshape(3,1)
## 특성 정규화(Feature Normalization)
# 신경망 학습과정 중에 정규화가 진행되나 지금은 빠른 수렴을 위해 특성을 정규화하여 진행하겠습니다.
X = X / np.amax(X, axis=0) # 최대값으로 나눠 0-1사이의 값으로 만들어 줌
y = y / np.amax(y, axis=0)
print("공부시간, 수면시간 \n", X)
print("시험점수 \n", y)
공부시간, 수면시간
[[1. 1. ]
[0.25 0.625]
[0.875 0.75 ]]
시험점수
[[1. ]
[0.35714286]
[0.83928571]]신경망 클래스 내 init 메소드에서 신경망의 구조를 결정합니다.
# Neural network를 정의하는 Class를 제작하는 코드입니다.
class NeuralNetwork:
def __init__(self):
# 신경망의 구조를 결정합니다. 입력층 2 노드, 은닉층 3 노드, 출력층 1 노드
self.inputs = 2 # 입력노드 수
self.hiddenNodes = 3 # 히든노드 수
self.outputNodes = 1 # 출력노드 수
# 가중치를 초기화 합니다.
# layer 1 가중치 (2x3)
self.w1 = np.random.randn(self.inputs,self.hiddenNodes)
# np.random.randn(m,n)는 가우시안 표준 정규 분포(평균 0, 표준편차 1)에서 난수 matrix array(m,n) 생성
# layer 2 가중치 (3x1)
self.w2 = np.random.randn(self.hiddenNodes, self.outputNodes)
# 정의된 클래스를 사용해보고, 해당 가중치를 디스플레이 하는 코드입니다.
nn = NeuralNetwork()
print("Layer 1 가중치: \n", nn.w1)
print("Layer 2 가중치: \n", nn.w2)
Layer 1 가중치:
[[ 2.48783189 0.11697987 -1.97118428]
[-0.48325593 -1.50361209 0.57515126]]
Layer 2 가중치:
[[-0.20672583]
[ 0.41271104]
[-0.57757999]]참고) [l x m] * [m x n] = [l x n] 행렬의 형태로 연산이됩니다
순방향 기능 구현
순방향 전파 기능 구현 후 신경망은 출력값을 내보낼 수 있게 됩니다.
# Neural network class를 기능을 추가하여 다시 정의하는 코드입니다.
# "def feed_forward(self, X):"부분을 추가로 정의한 것을 볼 수 있습니다.
class NeuralNetwork:
def __init__(self):
# 신경망의 구조를 결정합니다. 입력층 2 노드, 은닉층 3 노드, 출력층 1 노드
self.inputs = 2
self.hiddenNodes = 3
self.outputNodes = 1
# 가중치를 초기화 합니다.
# layer 1 가중치 (2x3)
self.w1 = np.random.randn(self.inputs,self.hiddenNodes)
# layer 2 가중치 (3x1)
self.w2 = np.random.randn(self.hiddenNodes, self.outputNodes)
def sigmoid(self, s):
return 1 / (1+np.exp(-s))
def feed_forward(self, X):
# 가중합 계산
self.hidden_sum = np.dot(X, self.w1)
# 활성화함수
self.activated_hidden = self.sigmoid(self.hidden_sum)
# 출력층에서 사용할 은닉층의 각 노드의 출력값을 가중합 합니다.
self.output_sum = np.dot(self.activated_hidden, self.w2)
# 출력층 활성화, 예측값을 출력합니다.
self.activated_output = self.sigmoid(self.output_sum)
return self.activated_output# 예측을 수행해 봅시다.
nn = NeuralNetwork()
print(X[0])
output = nn.feed_forward(X[0])
print("예측값: ", output)
[1. 1.]
예측값: [0.21945787]
# 수면, 공부시간(x[0])에 따른 타겟값인 1 (y[0])에 가깝게 나와야되는데 수치가 꽤 다른값이 나옴Error 계산
error = y[0] - output
error
array([0.78054213])# 모든 데이터를 예측해보고 에러값을 계산해 보겠습니다.
# print(X)
output_all = nn.feed_forward(X)
error_all = y - output_all
print(output_all)
print(error_all)
[[0.21945787]
[0.34573206]
[0.23788921]]
[[0.78054213]
[0.0114108 ]
[0.6013965 ]]에러값이 높게 나오는 이유는 무엇일까요?
- 에러가 높은 이유는 예측값이 낮게(정확하지 않게) 나오기 때문입니다.
예측값이 낮게 나오는 이유는 무엇일까요?
- Random으로 가중치를 만들었기 때문이고, 조금 더 자세히 말하면,
- 두번째 층의 가중치값(w2)들이 낮기 때문이거나
- 첫번째 층의 출력값(activatedHidden1∗w2)이 낮기 때문입니다.
첫번째 층의 출력값(hiddenSum1)은 어떤 값들의 계산으로 나오게 되나요?
- 입력값(고정, 변하지 않음)
- 가중치(variable, parameters)
이 두 변수의 가중합으로 이루어 집니다.
입력값은 고정값이기 때문에 이 상황에서 예측값을 증가시키기 위한 방법은 첫번째 층과 두번째층의 가중치를 증가하는 방법밖에 없습니다.
각 층의 노드들 마다 가중치가 존재하는데요, 원하는 결과를 얻기 위해서는 어떤 가중치를 얼마만큼 올려주는 것이 가장 효과적일까요?
이미 높은 활성화값을 가지고 있는 노드의 가중치를 올리면 상대적으로 큰 효과가 없을 것 입니다.
어떤 층의 어떤 노드들의 가중치를 얼마나 올려야 할까요?
한번 가중치들을 눈으로 살펴 보겠습니다.
# 각각의 변수들을 디스플레이 하기위한 코드입니다.
attributes = ['w1', 'hidden_sum', 'activated_hidden', 'w2', 'activated_output']
for i in attributes:
if i[:2] != '__':
print(i+'\n', getattr(nn,i), '\n'+'---'*3)
w1
[[-1.75351135 1.23279898 0.24464757]
[-0.06568225 0.30190098 0.79723428]]
---------
hidden_sum
[[-1.8191936 1.53469996 1.04188185]
[-0.47942924 0.49688786 0.55943332]
[-1.58358412 1.30512484 0.81199233]]
---------
activated_hidden
[[0.13953066 0.82269293 0.73921295]
[0.38238691 0.62172769 0.63632141]
[0.17028848 0.78669622 0.6925339 ]]
---------
w2
[[ 1.23073545]
[-1.52187331]
[-0.25502715]]
---------
activated_output
[[0.21945787]
[0.34573206]
[0.23788921]]
---------Error를 줄이기 위해서는?
- 경사(Gradient)를 계산해서 경사가 작아지도록 가중치를 업데이트!

위의 신경망 알고리즘 단계 2,3,4를 주어진 배치에 해당하는 모든 관측치에 대해 적용을 합니다.
비용함수의 기울기와 연관된 가중치를 업데이트 합니다.
우리 신경망은 전체 9개의 가중치를 가지고 있습니다.(첫번째 층 6개, 두번째 층 3개)
그러므로 경사하강법에서 나오는 기울기는 어떤 9차원 공간의 함수에서 가장 아래쪽 방향(오류를 줄이는 방향)으로 향하는 벡터가 될 것입니다.
네트워크에 9 개의 가중치가 있으므로 경사 하강 계산에서 나오는 기울기는 9 차원 공간의 일부 기능을 따라 가장 아래쪽 방향으로 이동하는 벡터가됩니다.
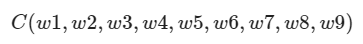
물론 여러분이 생각해야 할 것은 복잡한 신경망 모델은 대부분 convex 함수가 아니라는 것입니다.
그래서 경사하강법은 종종 지역 최소값에 빠질 수 있다는 것입니다.
(단순히 오목한 그래프가 아니라, 아래와 같은 그래프일것이다.)

물론 이런 문제를 해결하기 위한 여러가지 방법이 있습니다. 경사하강법의 다양한 알고리즘과 데이터를 어떻게 사용하여 이 방법을 이용할 지에 대해서는 아래에서 추가적으로 설명하겠습니다.
** Convex & Concave Function (볼록 & 오목 함수)
# 음수 가중치를 가지는 활성화는 낮추고, 양수 가중치를 가지는 활성화는 높이고 싶습니다.
class NeuralNetwork:
def __init__(self):
# 신경망의 구조를 결정합니다. 입력층 2 노드, 은닉층 3 노드, 출력층 1 노드 / Bias 없음.
self.inputs = 2
self.hiddenNodes = 3
self.outputNodes = 1
# 가중치를 초기화 합니다.
# layer 1 가중치 (2x3)
self.w1 = np.random.randn(self.inputs,self.hiddenNodes)
# layer 2 가중치 (3x1)
self.w2 = np.random.randn(self.hiddenNodes, self.outputNodes)
def sigmoid(self, s):
return 1 / (1+np.exp(-s))
def sigmoidPrime(self, s):
sx = self.sigmoid(s)
return sx * (1-sx)
def feed_forward(self, X):
# 가중합 계산
self.hidden_sum = np.dot(X, self.w1)
# 활성화함수
self.activated_hidden = self.sigmoid(self.hidden_sum)
# 출력층에서 사용할 은닉층의 각 노드의 출력값을 가중합 합니다.
self.output_sum = np.dot(self.activated_hidden, self.w2)
# 출력층 활성화, 예측값을 출력합니다.
self.activated_output = self.sigmoid(self.output_sum)
return self.activated_output
#### feed_forward까지는 이전 코드와 같습니다.
def backward(self, X, y, o):
# 역전파 알고리즘
# 출력층의 손실값 (Error) 입니다.
self.o_error = y - o # y와 계산된 output의 차이
# 출력층 활성화함수인 시그모이드 함수의 도함수를 사용합니다. (dE / dY * dY / dy) - Latter A
self.o_delta = self.o_error * self.sigmoidPrime(o)
# z2 error: 출력층의 가중치가 얼마나 에러에 기여했는지
self.z2_error = self.o_delta.dot(self.w2.T)
# z2 delta: 시그모이드 도함수를 z2 error에 적용합니다. (d_HiddenE / dY) * (dY / dy) - Latter
self.z2_delta = self.z2_error*self.sigmoidPrime(self.output_sum)
# w1를 업데이트 합니다.
self.w1 += X.T.dot(self.z2_delta) # X * dE/dY * dY/dy(=Y(1-Y))
# w2를 업데이트 합니다.
self.w2 += self.activated_hidden.T.dot(self.o_delta) # H1 * Y(1-Y) * (Y - o) # (Latter A)
def train(self, X,y):
o = self.feed_forward(X)
self.backward(X,y,o)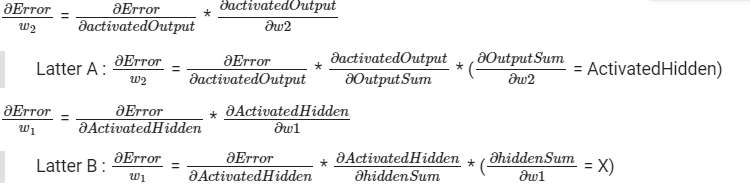
출력층 Error에서부터 시작
nn = NeuralNetwork()
nn.train(X,y)
# 출력층 에러를 확인해봅니다.
nn.o_error
array([[0.70644301],
[0.10036169],
[0.56649547]])출력층 Gradient 계산 (기울기)
시그모이드 활성함수가 변화에 얼마나 영향을 줄까요?
self.o_delta = self.o_error * self.sigmoidPrime(self.output_sum)
nn.output_sum
##
array([[-0.87817076],
[-1.0627663 ],
[-0.9805118 ]])
nn.sigmoid(nn.output_sum)
##
array([[0.29355699],
[0.25678117],
[0.27279024]])
# 출력층과 은닉층 사이 가중치(w2)가 얼마나 변화되어야 하는지 알려줍니다
nn.o_delta
##
array([[0.17285985],
[0.02468133],
[0.13902149]])은닉층 에러
은닉층 출력값을 곱한 에러 전파량을 계산
self.z2_error = self.o_delta.dot(self.w2.T)
토론: 은닉층 에러값 모양인 shape(3,3)에 대해 설명해 보세요
3*3인 이유는 은닉층 layer1 2*3 에서 layer2 3*1로 넘어가는 에러를 확인해서입니다.
nn.o_delta.dot(nn.w2.T)
##
array([[-0.28194591, -0.23236088, 0.12295841],
[-0.04025689, -0.03317703, 0.01755629],
[-0.22675329, -0.18687483, 0.09888856]])은닉층 Gradient 계산
각 관측치에 대해 어떤 활성화 출력이 올바른 예측에 영향을 주었을까요?
self.z2_delta = self.z2_error * self.sigmoidPrime(self.activated_hidden)
nn.activated_hidden
###
array([[0.43460965, 0.23985861, 0.42340322],
[0.37111212, 0.48687214, 0.52242758],
[0.48093658, 0.2520165 , 0.4192448 ]])
nn.z2_delta
###
array([[-0.06388859, -0.05136035, 0.020324 ],
[-0.00839476, -0.00674859, 0.00267051],
[-0.04915074, -0.03951252, 0.01563565]])
X.T.shape == nn.w1.shape
###
TrueGradient Descent 방식으로 업데이트
은닉층 가중치 업데이트
- 왜 입력값과 기울기값들을 곱해야 할까요? 가중치를 업데이트 하기위해서
- 왜 입력값을 transpose 해야 할까요? transpose 해야 벡터들의 곱연산이 가능해진다
X.T
###
array([[1. , 0.25 , 0.875],
[1. , 0.625, 0.75 ]])
X.T.dot(nn.z2_delta)
###
array([[-0.10899418, -0.08762095, 0.03467281],
[-0.10599837, -0.0852126 , 0.0337198 ]])출력층 가중치 업데이트
- 왜 출력층 은 3x1 모양을 가질까요? 출력노드가 3개이기 때문
- 왜 첫번째층 출력값과 기울기를 곱해야 할까요? 첫번째층 출력값이 두번째층 입력값이 되기때문이다
nn.activated_hidden.T.dot(nn.o_delta)
###
array([[0.15114662],
[0.08851428],
[0.14436766]])Backpropagation 리뷰 with Math






Keras를 이용한 역전파 실습
케라스(https://keras.io)는 거의 모든 종류의 딥러닝 모델을 간편하게 만들고 훈련시킬 수 있는 파이썬 딥러닝 프레임워크입니다.
케라스는 딥러닝 모델을 만들기 위해 고수준의 구성 요소를 제공하는 모델 수준의 라이브러리입니다.
텐서의 조작이나, 미분 등 low level단의 연산을 더이상 만들거나 하지 않아도 됩니다.
여러 백엔드 엔진(Tensorflow, Theano, Microsoft Cognitive Toolkit(CNTK))에서 제공하는 특화된 텐서 라이브러리를 사용하여 우리가 공부했던 내용을 자동화된 방식으로 활용할 수 있습니다.
한편, 케라스는 CPU, GPU 모두 동일한 코드로 실행할 수 있습니다.
모델을 정의하는 방법 중 Sequential 방법은 가장 자주 사용하는 구조인 층(layer)을 순서대로 쌓아 올린 네트워크 입니다.
이 방법은 다음과 같은 작업 흐름을 가집니다.
- 학습 데이터 로드
- 모델 정의
- 컴파일(Compile)
- 모델 학습(Fit)
- 모델 검증(Evaluate)
앞으로 케라스로 신경망을 만들 때 이 흐름을 잘 기억해 두시기 바랍니다.
# 앞서 살펴본 선형 데이터를 만들기 위함 함수
def make_samples(n=1000):
study = np.random.uniform(1, 8, (n, 1))
sleep = np.random.uniform(1, 8, (n, 1))
y = 5 * study + 2 * sleep + 40
X = np.append(study, sleep, axis = 1)
# 정규화
X = X / np.amax(X, axis = 0)
y = y / 100
return X, yimport numpy as np
import matplotlib.pyplot as plt
X, y = make_samples()
X[:10]
###
array([[0.76155759, 0.4065224 ],
[0.78699611, 0.19627527],
[0.39267953, 0.53940436],
[0.36391073, 0.99427628],
[0.64412524, 0.48054391],
[0.22616247, 0.13942684],
[0.70853207, 0.3407582 ],
[0.85016525, 0.44315516],
[0.26123166, 0.63737043],
[0.94228448, 0.48463672]])# !pip install tensorflow-gpu==2.0.0-rc1
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
model = Sequential()
# 신경망 모델 구조 정의
model.add(Dense(3, input_dim=2, activation='sigmoid'))
model.add(Dense(1, activation='sigmoid'))
# 컴파일 단계, 옵티마이저와 손실함수, 측정지표를 연결해서 계산 그래프를 구성을 마무리 합니다.
model.compile(optimizer='sgd', loss='mse', metrics=['mae', 'mse'])
# model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy']) # 분류인 경우 예시
results = model.fit(X,y, epochs=50)
###
Epoch 48/50
32/32 [==============================] - 0s 1ms/step - loss: 0.0097 - mae: 0.0832 - mse: 0.0097
Epoch 49/50
32/32 [==============================] - 0s 1ms/step - loss: 0.0098 - mae: 0.0848 - mse: 0.0098
Epoch 50/50
32/32 [==============================] - 0s 1ms/step - loss: 0.0091 - mae: 0.0806 - mse: 0.0091results.history.keys()
###
dict_keys(['loss', 'mae', 'mse'])plt.plot(results.history['loss'])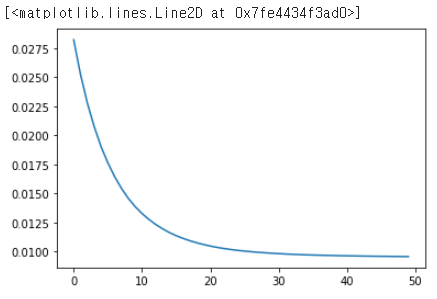
plt.plot(results.history['mae'])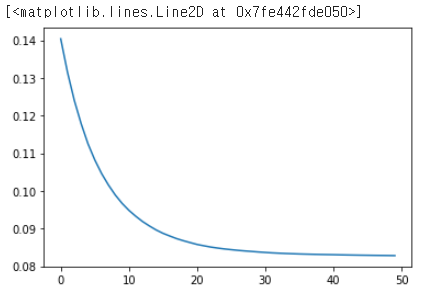
요약
이전 글에서 설명했듯이 활성화 함수를 적용시킨 MLP에서 XOR과 같은 non-linear 문제들은 해결할 수 있었지만 layer가 깊어질수록 파라미터의 개수가 급등하게 되고 이 파라미터들을 적절하게 학습시키는 것이 매우 어려웠다.
그리고 이는 역전파 알고리즘이 등장하게 되면서 해결되었고 결론적으로 여러 layer를 쌓은 신경망 모델을 학습시키는 것이 가능해졌다.
<역전파>
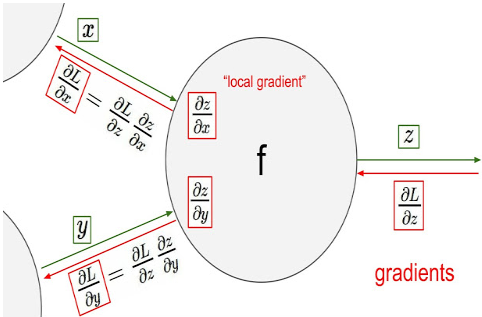
역전파 알고리즘은 출력값에 대한 입력값의 기울기(미분값)을 출력층 layer에서부터 계산하여 거꾸로 전파시키는 것이다.
이렇게 거꾸로 전파시켜서 최종적으로 출력층에서의 output값에 대한 입력층에서의 input data의 기울기 값을 구할 수 있다.
이 과정에는 중요한 개념인 chain rule이 이용된다.
출력층 바로 전 layer에서부터 기울기(미분값)을 계산하고 이를 점점 거꾸로 전파(역전파)시키면서
전 layer들에서의 기울기와 서로 곱하는 형식으로 나아가면 최종적으로 출력층의 output에 대한 입력층에서의 input의 기울기(미분값)을 구할 수가 있다. 이는 위의 그림에서 설명한바와 같다.
역전파 알고리즘이 해결한 문제가 바로 파라미터가 매우 많고 layer가 여러개 있을때 가중치w와 b를 학습시키기 어려웠다는 문제이다. 그리고 이는 역전파 알고리즘으로 각 layer에서 기울기 값을 구하고 그 기울기 값을 이용하여 Gradient descent 방법으로 가중치w와 b를 update시키면서 해결된 것이다.
즉, layer에서 기울기 값을 구하는 이유는 Gradient descent를 이용하여 가중치를 update하기 위함이다.
이때 각 layer의 node(parameter)별로 학습을 해야하기 때문에 각 layer의 node별로 기울기 값을 계산해야하는 것이다.

하지만 GD방식도 단점이 있었고, 이를 해결하기위한 다양한 Optimizer가 나왔습니다.
'데이터 분석 > 딥러닝' 카테고리의 다른 글
| [python] ArgumentParser(argparse) 정리 (0) | 2023.08.03 |
|---|---|
| Compound Scaling (0) | 2021.11.18 |
| Optimizer, Loss Funtion (0) | 2021.04.08 |
| Neural Network (0) | 2021.04.06 |


