머신러닝은 CS231n의 강의순서대로 정리할 예정입니다.
현재는 중간고사가 끝난 상태라 애매하게 CNN부터 포스팅을 시작하지만 나중에 강의목록 전체를 정리하겠습니다.
퍼셉트론, 역전파, loss 및 activation function, optimization, regularization 에 대한 지식이 필요합니다.
개인 정리용이므로 왠만하면 다른 포스트보는걸 추천합니다 :)
Fully connected Neural Network (대표적인 Neural Networks)

Fully connected Neural Network은 한 계층(layer)의 모든 뉴런을 다른 계층의 모든 뉴런에 연결하는 일련의 완전히 연결된 계층(layer)으로 구성됩니다.
- 주요 장점은 "구조에 구애받지 않는것"입니다. 즉, 입력에 대해 특별한 가정이 필요하지 않습니다.
- 구조에 구애받지 않기 때문에 매우 광범위하게 적용할 수 있지만, 입력 구조에 맞춰 조정된 특수 목적 네트워크보다 성능이 떨어지는 경향이 있습니다.
특히 3개의 채널(RGB)로 구성된 이미지 파일을 다룰때 성능이 크게 떨어집니다.
Fully Connected Layer(FCL)에서 이미지가 input으로 들어왔을때 어떻게 처리하는지 살펴보겠습니다.

32*32*3 사이즈의 image 파일을 input으로 받게 되면 FCL은 input을 flat하게 stretch해서 1 * 3072의 벡터로 만듭니다.
그리고 가중치 W(10x3072 행렬)를 input 벡터와 곱하여 얻는 한줄의 dot product(Wx)를 activiation 처리하여
FCL의 출력값을 얻습니다. (이 예시의 경우 10개의 출력값)
위의 FCL처럼 input을 flat하게 처리할 경우 이미지가 갖는 spatial(공간적)특징을 잃게 됩니다.
Convolutional Neural Networks(CNN)에서는 Convolutional Layer 단계에서 필터로 이미지 input을 처리하여 spatial한 특징을 유지해서 위 문제를 해결할 수 있습니다.
Convolutional Neural Networks(CNN)

CNN은 convolution layer와 pooling layer를 반복하는 architecture 입니다.
위 특히 convolution layer가 novel idea인데, 이를 통해서 input의 spatial한 특성은 유지하면서 Feature extraction 합니다.
먼저 convolution layer가 어떻게 input을 처리하길래 FCL과 다른지 살펴 보겠습니다.
Convolution layer

먼저 Convolution(Conv)은 수학적 연산이며, 정의에 따르면 두 함수를 결합하여 세 번째 함수를 얻는 방법입니다.
앞서 말했듯이 Convolution Layer는 Fully Connected Layer와 달리 input의 구조를 그대로 유지한채로 feature extract합니다. spatial한 특성을 유지하는건 필터(kernel)를 가중치로 사용하기 때문입니다.
Convolution Layer에서는 필터를 가지고 input 이미지를 슬라이딩하면서 공간적으로 내적(dot product)을 수행하게 됩니다.
이때 필터는 input 이미지의 깊이(depth)만큼 확장됩니다.(즉 항상 input의 depth와 filter의 depth는 동일합니다.)
w*h*d 크기의 input image에 n*n 크기의 filter를 사용하여 Conv한다면
filter의 depth는 자동으로 input image의 depth와 같아져서 n*n*d 크기를 갖는 filter가 된다고 생각하면 됩니다.

필터를 이미지의 공간에 겹쳐놓고 필터의 각 w와, 이에 해당하는 이미지의 픽셀을 곱해줍니다.
이는 W^t * x + b를 수행하는 것과 같습니다. --- (1)
필터가 슬라이딩 할 때, Convolution은 이미지의 좌상단부터 시작합니다.
필터의 모든 요소를 가지고 내적(dot product)을 수행하게 되면 하나의 값을 얻게됩니다.
위 과정을 모든 input에 대해 슬라이딩하며 연산하고, 결과 값을 output에 저장합니다.
하나의 채널(depth)만 따로 빼서 보면 다음과 같습니다.

Convolution은 수학적 연산이며 정의에 따르면 두 함수를 결합하여 세 번째 함수를 얻는 방법입니다.
- 첫 번째 함수는 입력 이미지(5*5)입니다.
- 두 번째 함수는 이미지 위를 미끄러지는 필터 (3*3 행렬)입니다.
- 출력 또는 세 번째 함수는 output 이미지(3*3)입니다.

필터는 입력 레이어 위로 이동하고 각 단계에 대해 필터의 요소와 이미지 값의 곱(Convolution)이 수행됩니다.
각 픽셀에 대해 합산된 값을 출력 레이어에 저장합니다. (동일한 작업을 반복적으로 수행)

즉, (1) 식을 통해 나온 값들을 activation map에 해당하는 위치에 저장합니다.
이때 출력 activation map 의 크기는 input과 filter의 크기에 의해 결정됩니다.
(위 output은 stride가 1, zero-padding은 0임을 가정하고 계산한 결과입니다.)
- output size = {(input size - filter size + 2 * padding size) / stride size} + 1입니다.
- 28 = {(32 - 5 + 0) / 1} + 1
참고로 padding, stride는 feature map 크기를 조정하는 Conv 기법으로 사용자의 목적에 따라 달리 사용됩니다.
(filter의 크기와 동일하게 사용자가 지정하는 hyper parameter)
stride를 늘리면 output의 크기를 많이 축소시켜서 파라미터의 수를 줄일 수 있고,(계산 속도 빨라짐)
padding을 추가하면 윤곽데이터를 보존하고, output의 크기를 유지할 수 있습니다.
또한 패딩을 추가한다고 해도 네트워크 표현력을 추가하는것이지, 망치지 않는다고 하네요
(Conv를 거듭할수록 feature 크기가 줄어드는데, 계산할 수 없을정도로 너무 작아지는걸 방지)
추가 예시) output volume size, Number of learnable parameters and multiply-add operations
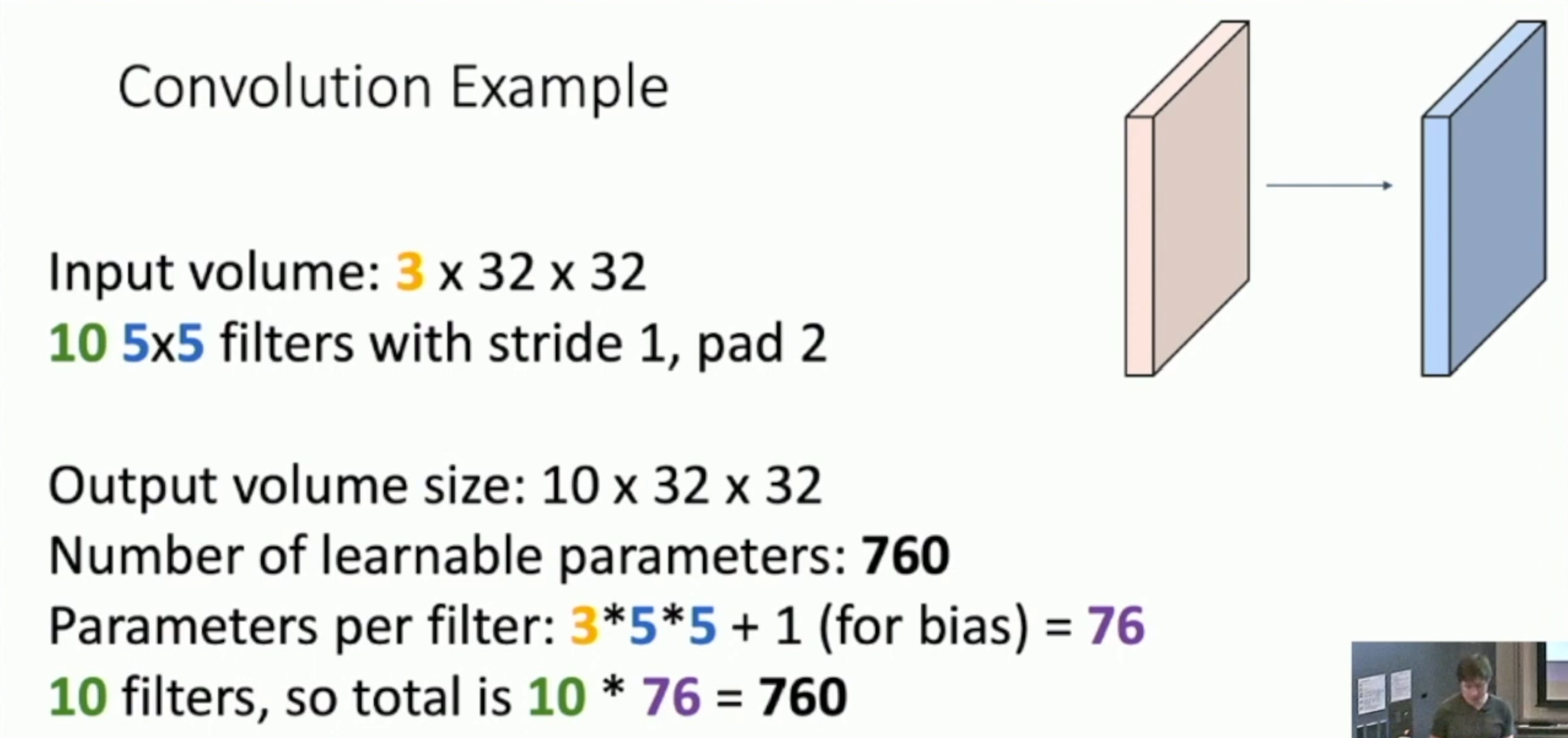

파라미터는 가중치와 bias, Conv Layer에서는 filter와 bias를 의미한다는걸 잊으면 안됩니다.
또한 Layer에서는 각 filter의 가중치를 공유한다는 것도 중요합니다.
그리고 필터의
다시 본론으로 돌아와서 일반적으로 convolution layer에서는 filter를 여러개를 사용합니다.
이는 filter 하나당 이미지에서 하나의 특성을 추출하는데, 우리는 여러개의 filter를 사용해서 다양한 특성을 추출하기 위함입니다.

위의 예시에서는 6개의 필터를 사용해서 28*28*6의 크기를 갖는 Output이 생성됐습니다.
여기서 알 수 있듯이 Output의 depth는 필터의 개수와 동일합니다!
즉 CL의 Output은 activation map(feature map)을 필터의 개수만큼 모은 형태입니다.
이는 Input의 구조적 형태처럼 3차원의 tensor를 갖는 Output이 생성되므로 FCL과 달리 Convolution Layer는
Input의 Spatial한 구조를 유지하는 Output을 출력한다고 볼 수 있습니다.
Convolution Layer 에서의 Batch Normalization(BN)

BN은 Layer가 쌓일수록 생기는 vanishing/exploding gradient 문제를 해결하고, 학습 시간을 크게 줄일 수 있을 뿐만 아니라, 학습의 정확도도 개선할 수 있어서 대부분의 모델에 적용됩니다.
BN은 활성 함수의 종류와 상관없이 적용이 가능하다. 활성 함수를 g라고 하고, 가중치를 W, 입력 데이터를 u, 바이어스를 b라고 하면, 다음은 기본 신경망을 표현하는 함수 형태가 됩니다.
z = g(Wu + b)
non-linearity 함수 g 앞에 BN을 적용하게 되면, 결과적으로 x = Wu + b를 정규화 하는 것이 된다. Wu + b에 BN을 적용하면, 정규화 후 scale과 shift 항을 학습을 통해 결정하는데, b는 shift 항으로 대체할 수 있기 때문에 b는 무시할 수 있으며, 앞 선 식을 다시 정리하면 아래와 같은 형태가 된다.
z = g(BN(Wu ))
여기서 BN transform은 각각의 activation에 x = Wu에 독립적으로 적용하며, 또한 학습을 통해 변수 γ와 β가 쌍으로 결정이 된다.
하지만 convolutional layer에 적용할 때는 조금 달라지는 부분이 있는데, 이는 convolution의 특성을 살리기 위함이다. Convolutional layer에서는 shared weight와 sliding window 방식을 적용하여 출력 feature-map의 모든 픽셀에 대하여 동일한 연산을 수행한다. 마찬가지로 BN을 적용할 때는 mini-batch에 있는 모든 activation 뿐만 아니라 모든 위치까지 함께 고려해줘야 한다.
BN을 convolutional layer에 적용을 할 때 mini-batch의 크기를 m이라고 하고, 출력 feature-map의 크기를 p x q라고 하면, 출력 feature-map의 크기에 해당하는 만큼 sliding window를 움직이면서 연산을 해주기 때문에 mini-batch의 크기가 사실상 m’ = m x p x q로 커진 것으로 간주하고 평균과 분산을 구한다.
γ와 β는 fully connected의 경우처럼 activation마다 붙는 것이 아니라, feature-map에 대하여 γ와 β쌍이 학습을 통해 결정이 된다.
(BN 설명 출처 - https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=laonple&logNo=220811172205)
요약 (https://eehoeskrap.tistory.com/430)
컨볼루션 레이어에서 활성화 함수가 입력되기 전에 Wu + b 로 가중치가 적용되었을 때, b의 역할을 베타가 완벽히 대신 할 수 있기 때문에 b 를 삭제한다.
또한 CNN의 경우 컨볼루션 성질(spatial한 feature)을 유지 시키고 싶기 때문에 각 채널을 기준으로 각각의 감마와 베타를 만들게 된다.
예를 들어 미니배치가 m 채널 사이즈가 n 인 컨볼루션 레이어에서 배치 정규화를 적용하면 컨볼루션을 적용한 후의 특징 맵의 사이즈가 p x q 일 경우, 각 채널에 대해 m x p x q 개의 스칼라 값(즉, n x m x p x q 개의 스칼라 값)에 대해 평균과 분산을 구한다.
최종적으로 감마 베타 값은 각 채널에 대해 한 개씩, 총 n개의 독립적인 배치 정규화 변수 쌍이 생기게 된다.
즉, 컨볼루션 커널 하나는 같은 파라미터 감마, 베타를 공유하게 된다.
Convolution Layer의 특징을 유지하기 위해 Regularization 기법도 변형한다는걸 보여주기 위해 설명을 추가했습니다.
이전까지의 설명들을 중간 정리하자면 다음과 같습니다.
Convolution Layer(CL)의 가중치에 해당하는 filter의 depth는 input의 depth와 같다.
(input과 filter를 내적해서 activation map(feature map)을 만들어야 되기 때문)
그리고 filter의 개수에 따라 activation map의 depth가 정해진다.
위 과정을 거치기 때문에 input의 spatial한 구조를 output에서도 유지할 수 있다.
또한 batch normalization 과정을 거쳐도 spatial한 구조를 유지한다.
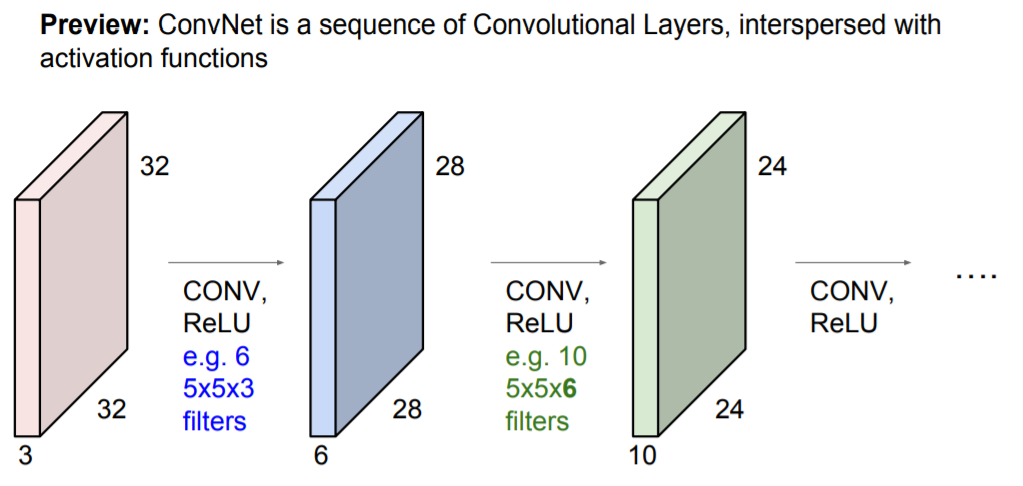
제일 처음 CNN의 구조를 보여줬던 사진에 나와있듯이 CNN은 Convolution Layer의 연속된 형태 입니다.
각 Conv Layer는 여러개의 필터(가중치)를 가지고 있고, 필터마다 각각의 Output(activation map)을 만듭니다.
그 output에 activation function(ex.ReLU)을 적용한 것이 반복되는 Layer set이 됩니다. (가끔 Pooling layer도 포함됨)
(CL만 반복되면 하나의 CL과 다를게 없으므로 비선형 Layer인 activation function을 추가한것, FCL과 같은이유로 삽입)
각 Layer set의 출력이 output이 되고, 다음 Layer set의 입력이 되는 구조입니다.
그러므로 여러개의 Layer들을 쌓고나서 보면 layer의 각 필터들이 계층적(low to high level)으로 학습을 하는것을 볼 수 있습니다.
Alexnet을 봤을때 첫번째 Layer에 있는 필터들은 low-level feature(local image templates : 수직 또는 수평 edge, opposing color)를 학습합니다.

Conv Layer를 거칠수록 좀 더 복잡한 특징들을 추출합니다.
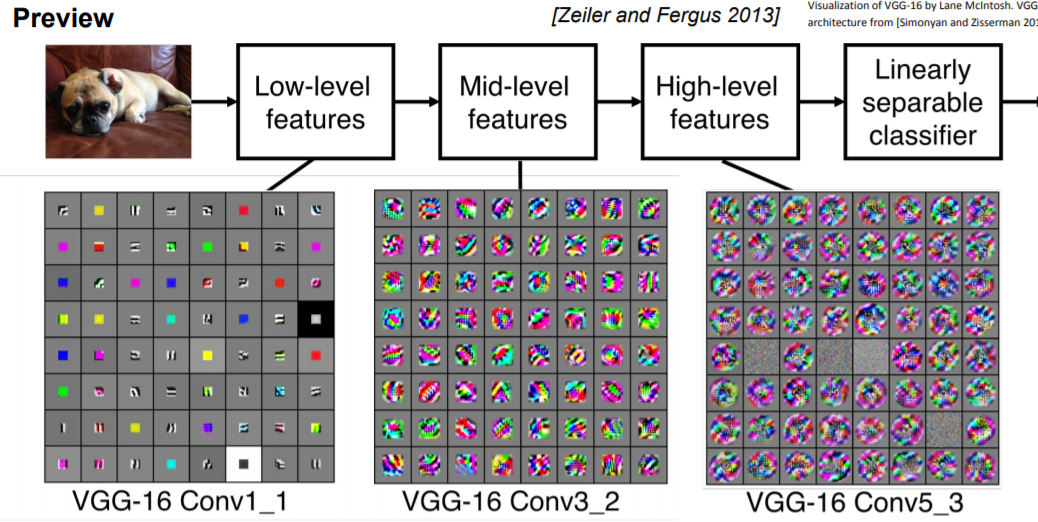
(참고로 위의 예시는 VGGnet입니다.)
이러한 특징은 Convolution의 특성 때문입니다.

초기에는 7*7 크기의 이미지가 3*3 크기의 필터를 거치면 5*5가 되고 한번 더 거치면 3*3이 됩니다.
low level의 지역적인 특징을 뽑아냈던걸 가지고, 또다시 특징을 뽑아내므로 갈수록 복잡한 feature를 뽑아내는거죠.
7*7사이즈의 input으로 예를들면 잘 와닿지 않을 수 있는데 요즘 이미지의 크기는 왠만하면 1024*1024의 크기를 갖고 있으므로 초기에는 정말 지역적인 feature만 찾는다는걸 깨달을 수 있으실겁니다.
Pooling Layer

Pooling Layer는 downsampling을 위해 존재합니다.
Downsampling을 하면 위와 같이 Representation이 작아집니다.
Max-Pooling 예시를 보는게 가장 이해가 빠를거 같아서 가져왔습니다.
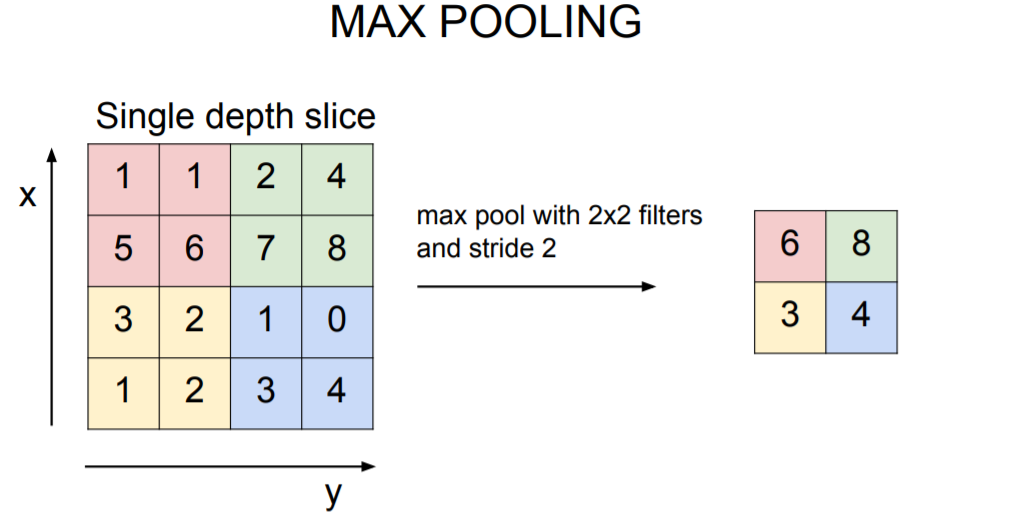
Pooling 기법은 avg pooling, max pooling 등 다양한 기법이 있습니다.
일반적으로 filter size는 2*2, stride를 2로 지정합니다.
Pooling Layer를 거치면 파라미터의 수가 줄게 되어 계산량이 줄고, 공간적인 불변성(invaiance)을 얻을 수 있습니다.
그리고 가장 중요한것은 Pooling Layer는 단순하게 downsampling 하는것이기 때문에 parameter가 없습니다!
추가로 invariance가 이해 안됐었는데 좋은 예시가 있어서 가져와봤습니다.
ex) 10*10 사람 얼굴 이미지가 있다고 했을때, (4,5)위치에 코가 있고, (6,5) 위치에 입이 있다고 칩시다.
Max-pooling을 하면 5*5 크기의 이미지로 변화하고, (2,3)위치에 코에 해당하는 픽셀이 있고, (3,3)위치에 입에 해당하는 픽셀이 있을겁니다.
위 상황이 이해됐다면, 새로운 이미지가 살짝 삐뚫어진 얼굴 이미지라고 가정해봅시다.
새로운 이미지에 (4,6)에 코가, (6,6)에 입이 있다고 해도, Max-Pooling을 하면 (2,3), (3,3)위치에 코와 입이 있을것이므로 이를 공간적 불변성을 갖는다고 합니다.
단, Pooling은 depth (깊이)에는 영향을 주지 않습니다.
만약 depth를 수정하고 싶다면 어떻게 해야될까요?
그에 대한 해답으로 1*1 Convolution을 하는 이유에 대해 알아보겠습니다.

앞서 설명했듯이 Output의 depth는 filter의 개수에 의해 결정됩니다.
그러므로 1*1 CONV은 Output의 행과 열을 변화시키지 않고 depth를 수정할때 쓰입니다.
일반적으로 depth를 감소시킬 때 쓰이지만, depth를 그대로 두고 쓰이는 경우도 있습니다.
이는 parameter의 개수를 늘려서 더 복잡한 네트워크로 만들기 위함입니다.
마지막으로 CONV-ReLU-Pooling을 반복해서 Feature extraction한 결과를 가지고 imager를 Classification 하기 위해
FCL을 거치면 CNN 완성입니다. (FCL을 안쓰는 CNN 모델도 많습니다.)

CNN 예시(Alexnet, VGGnet 등) 추가해야함
'Learning > 머신러닝' 카테고리의 다른 글
| Bayesian inference (0) | 2023.04.05 |
|---|