선형회귀(Linear Regression)
통계학에서, 선형 회귀는 종속 변수 y와 한 개 이상의 독립 변수 (또는 설명 변수) x와의 선형 상관 관계를 모델링하는 회귀분석 기법이다. 한 개의 설명 변수에 기반한 경우에는 단순 선형 회귀, 둘 이상의 설명 변수에 기반한 경우에는 다중 선형 회귀라고 한다.
선형 회귀는 선형 예측 함수를 사용해 회귀식을 모델링하며, 알려지지 않은 파라미터는 데이터로부터 추정한다. 이렇게 만들어진 회귀식을 선형 모델이라고 한다.
ko.wikipedia.org/wiki/%EC%84%A0%ED%98%95_%ED%9A%8C%EA%B7%80
선형 회귀 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 독립변수 1개와 종속변수 1개를 가진 선형 회귀의 예 통계학에서, 선형 회귀(線型回歸, 영어: linear regression)는 종속 변수 y와 한 개 이상의 독립 변수 (또는 설명
ko.wikipedia.org
※ Tabular data : 테이블 형식의 데이터로 행별로 어떤 것의 정보를 나타냅니다. 열별로 하나의 데이터 형식만 가질 수 있고, 행은 다양한 데이터형식을 가질 수 있다.
학습데이터에 따른 분류: Supervised learning vs Unsupervised learning
교사학습(Supervised learning)
- Goal: predict a single "target" or "outcome" variable y
- 입출력(input XX-outputyy)의 쌍으로 구성된 training data로부터 입력을 출력을 사상하는 함수를 학습하는 과정
- Method: Learn on training data, score on test data
- 즉, 입력벡터를 X, 그에 대응하는 출력벡터(i.e., label)를 y라고 할 때, training data는 D=(x,y)로 주어지게 되며, 모델은 이 training data에 기반하여 관측하지 않은 새로운 데이터 x′가 들어왔을 때 그에 해당되는 label, y′을 추론하는 방법을 배우게 된다
- ex: 분류(classification)와 회귀분석(regression)
비교사학습(Unsupervised learning)
- Goal: Explore intrinsic characteristics of data X
- Method: Estimate underlying distributions and/or segment data into meaningful groups or detect patterns
- There is no target (outcome) variable to predict or classify
- 출력값 없이 오직 입력값만 주어지며, 이러한 입력값들의 공통적인 특성을 파악하여 학습하는 과정
- Training data는 D=(x)로 주어지게 된다.
- ex: 군집화(clustering), 밀도추정(density estimation), 차원축소(dimension reduction)
특성공학(Feature Engineering)
적절한 feature들을 선정하기 위해서는 분석을 하는 목적을 잘 이해하고, 데이터의 의미를 잘 이해해야 합니다.
이 외에도 feature engineering이 힘든 이유는 feature 수가 매우 많아질 경우입니다. 많은 feature들 중 일부 feature는 결과에 중요한 영향을 주고, 많은 feature는 별 도움이 되지 않을 수 있습니다.
또한 feature들 사이에 의미가 매우 비슷한 것들도 있을 수 있어, 하나만 보존하고 나머지는 삭제하는 것이 좋습니다. 결과에 중요한 영향을 줄 feature들을 가려 내고, 의미가 비슷한 feature들을 가려 내는 일은 힘든 일입니다.
불필요한 feature들은 메모리 공간을 낭비하고 machine learning algorithm이 계산하는 시간만 길어지게 합니다.
(이런 경우를 일컬어 “curse of dimensionality” 또는 “feature explosion”이라고 합니다.)
Data partitioning
- 데이터를 training data와 test data로 나누는 것
- Training data: 모델 학습용
- Test data: 모델 성능 측정용
- 왜? Overfitting 방지, 일반화 성능 향상
- 보통은 60:40 정도로 데이터를 분할하지만, 보유하고 있는 데이터 규모에 따라 이 비율은 달라지기도 함
- 컴퓨터가 모델을 학습하고 평가 받는 것은, 교실에서 학생과 선생님 사이에서 발생하는 일과 매우 유사하다!
- Training phase: 교사는 문제(Xtrain)와 정답(ytrain)이 모두 포함된 training data를 이용해 컴퓨터를 훈련(training)시키고, 컴퓨터는 모델을 학습한다(learning).
- Testing phase: 컴퓨터가 training data로 모델을 학습한 후에는 교사가 컴퓨터에게 정답(ytest) 없이 문제(Xtest)만 포함된 시험(test data)을 전달한다. 이 때, 컴퓨터가 제출한 답안지(y^)와 실제 정답(ytest)간의 차이를 비교해서 오답/오류(error)가 얼마나 발생했는지 확인함으로써 모델의 성능/성적을 평가한다.
- 때로는 training data, validation data, test data 등 세 개의 그룹으로 데이터를 나누기도 함 (참고: What is the difference between test set and validation set?)

왜 같은 데이터셋 안에서 Training Data와 Test Data를 나누는 걸까요?
- 훈련데이터와 테스트데이터가 같으면 당연히 테스트결과가 좋기 때문에 다른데이터로 실험을 해야 신뢰성이 있다. 추가로 이전데이터를 학습해서 최근데이터를 테스트하는게 일반적이다.
Simple linear regression (SLR)
- Regression
- 대표적인 교사학습(supervised learning) 방법론
- "right answers" given
- Predict continuous valued output
- 대표적인 교사학습(supervised learning) 방법론
- Formulation
- x: 독립변수(independent variable)
- y: 종속변수(dependent variable)
- a,b: 파라미터(parameters) or 계수(coefficients)
- ϵ: Observation noise
- ex: Housing price prediction
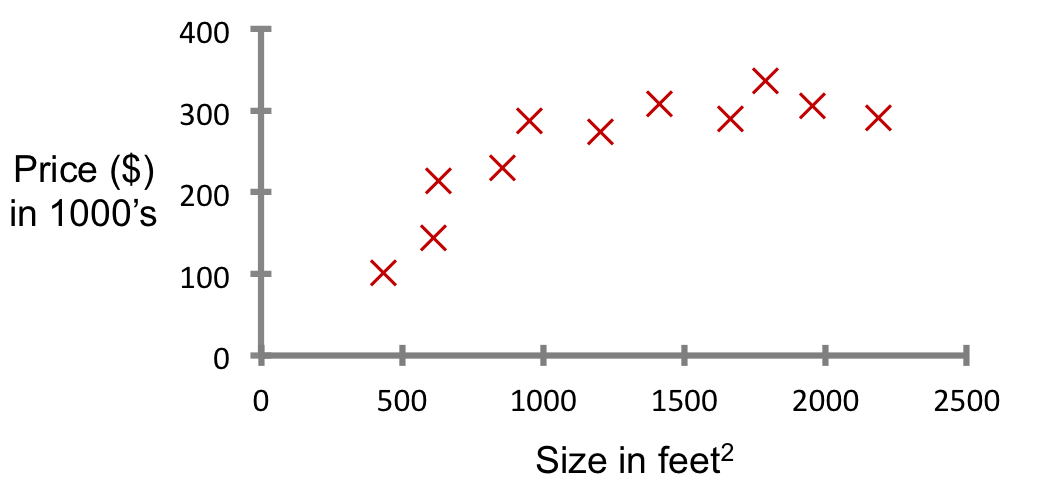
from sklearn.linear_model import LinearRegression
model = LinearRegression()
features = ['bathrooms'] # feature name ex) sqft_living, grade, ...
X_train = train[features]
X_test = test[features]
# 모델 fit
model.fit(X_train, y_train)
y_pred = model.predict(X_train)
# 데코레이터 interact를 추가합니다.
@interact
def explain_prediction1(bathrooms=(0,8)): # bathrooms 범위
y_pred = model_1.predict([[bathrooms]])
pred = f"{int(bathrooms)} bathrooms 주택 가격 예측: ${int(y_pred[0])} (1 bathroom당 추가금: ${int(model_1.coef_[0])})"
return predMultiple linear regression (MLR)
- Formulation
- xj: 독립변수들(independent variables)
- y: 종속변수(dependent variable)
- bj: 파라미터(parameters) or 계수(coefficients)
- ϵ: Observation noise
# Multiple linear regression
## 예측모델 인스턴스를 만듭니다
model_M = LinearRegression()
## X 특성들의 테이블과, y 타겟 벡터를 만듭니다
feature_M = ['sqft_living','bathrooms']
target_M = ['price']
X_train_M = df[feature_M]
y_train_M = df[target_M]
## 모델을 학습(fit)합니다
model_M.fit(X_train_M, y_train_M)
## 계수(coefficient) # slope coef
model_M.coef_
## 절편(intercept) # intercept coef
model_M.intercept_
# 데코레이터 interact를 추가합니다.
@interact
def explain_predictionM(sqft_living=(5000,1000000),bathrooms=(0,8)): # 두 특성의 범위
y_pred = model_M.predict([[sqft_living,bathrooms]])
pred = f"{int(sqft_living)} sqft_living과 {int(bathrooms)} bathrooms를 포함한 주택 가격 예측: ${int(y_pred[0,0])}"
return pred

'데이터 분석 > 전처리 및 EDA' 카테고리의 다른 글
| cheat sheet (0) | 2021.02.23 |
|---|---|
| Pandas란? (0) | 2021.01.26 |
| Pandas 기본설정 (0) | 2020.12.31 |

